Answer:
Option 2,4 are true statement.
Explanation:
Given : Function
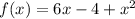
To find : Which statements are true about the graph of the function?
Solution :
First we have to convert the quadratic function
 into vertex form
into vertex form
 where (h,k) are the vertex.
where (h,k) are the vertex.
Function
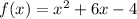
Applying completing the square i.e. add and subtract half square of b,
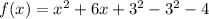
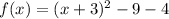
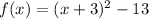
Option 1 is incorrect.
On comparing with vertex form,
h=-3 and k=-13
So, The vertex of the function is (h,k)=(-3,-13).
Option 2 is correct.
Axis of symmetry is
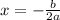
Substitute a=1 and b=6
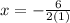

Option 3 is incorrect.
Now, We plot the graph of the function.
Refer the attached figure below.
The graph increases over the interval (–3,-13).
Option 4 is correct.
From the graph we see that it crosses x-axis.
Option 5 is incorrect.
Therefore, Option 2,4 are true statement.