Find the smallest possible value of a whole number 'y' if it leaves a remainder of 3 when divided by 5,6 or 9.

Question

asked Aug 4, 2020 177k views

1 Answer

Sinedsem · Answer 1 · 2020-08-09T23:45:57+0000

We want to find
such that

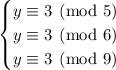
$\begin{cases}y\equiv3\pmod5\\y\equiv3\pmod6\\y\equiv3\pmod9\end{cases}$

6 and 9 are not coprime, so we split the moduli according to
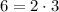$6=2\cdot3$ and
9=3^2 to get the system

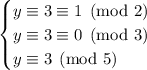
$\begin{cases}y\equiv3\equiv1\pmod2\\y\equiv3\equiv0\pmod3\\y\equiv3\pmod5\end{cases}$

If we take

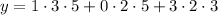
$y=1\cdot3\cdot5+0\cdot2\cdot5+3\cdot2\cdot3$

we can see that

taken mod 2, the last two terms vanish and we're left with
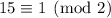$15\equiv1\pmod2$ ;
taken mod 3, the first and last terms vanish, and the remaining term is
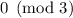$0\pmod3$ ;
taken mod 5, the first two terms vanish, and we're left with
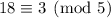
$18\equiv3\pmod5$

By the Chinese remainder theorem, we've found that any
satisfying

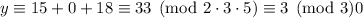
$y\equiv15+0+18\equiv33\pmod{2\cdot3\cdot5}\equiv3\pmod30$

will satisfy each congruence above, and that any solution of the form
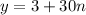y=3+30n for any integer
will work.

The smallest possible value of these occurs for
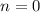n=0 , so that 3 is the least positive solution.