Question

PLEASE HELP ASAP!!! CORRECT ANSWER ONLY PLEASE!!!

Graph both functions to find the solution(s) to the system.

Answer 1

Answer: (-2, 5) and (2, -3)

Explanation:

Graph the line y = -2x + 1 (which is in y = mx + b format) by plotting the y-intercept (b = 1) on the y-axis and then using the slope (m = -2) to plot the second point by going down 2 and right 1 unit from the first point:

y - intercept = (0, 1) 2nd point = ( -1, 1).

Graph the parabola y = x² - 2x - 3 by first plotting the vertex and then plotting the y-intercept (or some other point):

`y = x^2-2x-3\quad \rightarrow \quad a=1,\ b=-2,\ c=-3\\\\\text{axis of symmetry:}\ x = (-b)/(2a)\ \longrightarrow \ x=(-(-2))/(2(1))=(2)/(2)=1\\\\\text{y-value of vertex:}\ f(1) = (1)^2-2(1)-3\quad \longrightarrow \quad y = 1 - 2 - 3=-4\\\\\text{y-intercept:}\ f(0)= (0)^2-2(0)-3\ \longrightarrow \ y=0 - 0 - 3 = -3 \\`

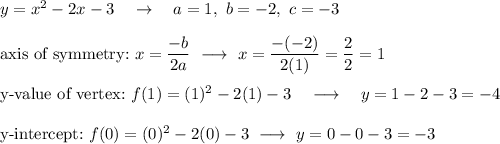
vertex = (1, -4) 2nd point (y-intercept) = (0, -3)

see attached - the graphs intersect at two points: (-2, 5) and (2, -3)