Answer:

This shows that the sum of the series varies directly as the number of terms.
Explanation:
The terms of the airthmetic series is given by .
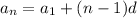
Where
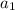 is the first term .
is the first term .
n represented the number of terms in the airthmetic series .
d is the common difference .
As given
If the first and the last terms of an arithmetic series are 10 and 62 .
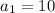
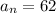
Putting in the above
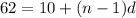
62 - 10 = (n-1)d
52 = (n-1)d
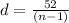
The Sum of the nth terms of the airthmetic series is given by .
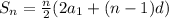
Putting the values in the above
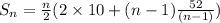
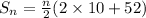
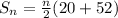
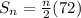
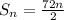

(This is for the n terms )
Therefore this shows that the sum of the series varies directly as the number of terms.