Question

If the first and the last terms of an arithmetic series are 10 and 62, show that the sum of the series varies directly as the number of terms.

Answer 1

`S_(n) = 36n`

This shows that the sum of the series varies directly as the number of terms.

Explanation:

The terms of the airthmetic series is given by .

`a_(n)=a_(1)+(n-1)d`

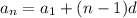
Where
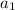`a_(1)` is the first term .

n represented the number of terms in the airthmetic series .

d is the common difference .

As given

If the first and the last terms of an arithmetic series are 10 and 62 .

`a_(1)= 10`

`a_(n)= 62`

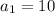
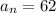
Putting in the above

`62=10+(n-1)d`

62 - 10 = (n-1)d

52 = (n-1)d

`d = (52)/((n-1))`

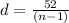
The Sum of the nth terms of the airthmetic series is given by .

`S_(n) = (n)/(2)(2a_(1)+(n-1)d)`

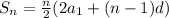
Putting the values in the above

`S_(n) = (n)/(2)(2* 10+(n-1)(52)/((n-1)))`

`S_(n) = (n)/(2)(2* 10+52)`

`S_(n) = (n)/(2)(20+52)`

`S_(n) = (n)/(2)(72)`

`S_(n) = (72n)/(2)`

`S_(n) = 36n`

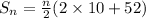
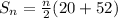
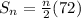
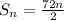
(This is for the n terms )

Therefore this shows that the sum of the series varies directly as the number of terms.