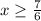Answer:
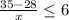
Explanation:
Let x be the average number of pounds Fido must loss.
Since, the initial weight of Fido is 35 pounds.
And, After losing the weight, the new weight of Fido in pounds = 28 pounds.
Then the time taken for losing the weight
=

=
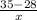
According to the question, it must lose weight within 6 months,
Thus,
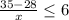
Which is the required inequality to find the average number of pounds per month.
By solving it we, get,