For this case we have the following quadratic equation
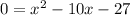 , which can be written like:
, which can be written like:
 , thus, it is of the form:
, thus, it is of the form:
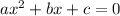
Where:
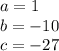
The roots will be:
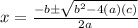
Substituting we have:
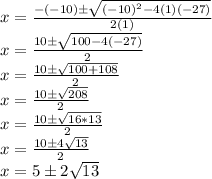
Thus, we have two solutions given by:

Answer:
The negative solution is between -3 and -2
The positive solution is between 12 and 13