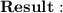Question

Determine the slope of a line that is perpendicular to the equation 3x + 6y =18

Answer 1

SOLVING

`\Large\maltese\underline{\textsf{A. What is Asked}}`

Determine the slope of the line perpendicular to 3x+6y=18

`\Large\maltese\underline{\textsf{B. This problem has been solved!}}`

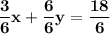`\bf{(3)/(6)x+(6)/(6)y=(18)/(6)` | dividing the ENTIRE equation by 6, to make it easier to write in y=mx+b form

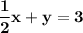`\bf{(1)/(2)x+y=3}` | subtract 1/2 x

`\bf{y=-(1)/(2)x+3`.

`\cline{1-2}`

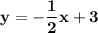Now, perpendicular lines' slopes are opposite inverses of each other.

The opposite inverse of -1/2 is

= 2

`\cline{1-2}`

`\bf{Result:}`

`\bf{=2}`

`\LARGE\boxed{\bf{aesthetics\\ot1\theta l}}`

Answer 2

Rewriting the equation of the given line in slope-intercept form,

`3x+6y=18\\\\x+2y=6\\\\2y=-x+6\\\\y=-(1)/(2)x+3`

This means the slope of the given line is -1/2.

As perpendicular lines have slopes that are negative reciprocals, the answer is 2.