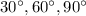Question

In a right triangle with a leg of 4 and a hypotenuse of 8, find the measures of all angles.

Answer 1

The measures of all angles are
`30\°,60\°,90\°`

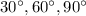
Explanation:

we know that

In a right triangle

Applying the Pythagoras theorem

`c^(2)=a^(2)+b^(2)`

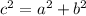
where

c is the hypotenuse

a,b are the legs

In this problem we have

`c=8\ units, a=4\ units`

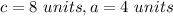
Find the value of b

`8^(2)=4^(2)+b^(2)`

`b^(2)=8^(2)-4^(2)`

`b^(2)=48`

`b=4√(3)\ units`

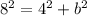
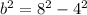
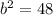
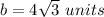
Remember that

A right triangle has a right angle and the other two angles are complementary

Let

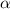`\alpha` ------> one of the two angles that are complementary

`\theta` ------> the second of the two angles that are complementary

so

`\alpha=arccos(a/c)=arccos(4/8)=60\°`

`\theta=arccos(b/c)=arccos(4√(3)/8)=30\°`

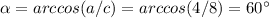
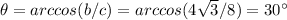
The measures of all angles are
`30\°,60\°,90\°`