Answer:
Let x represents the number of week and y represents the total number of book.
As per the given statement:
Kayla's classroom started out with a collection of only 18 books, but she plans to purchase an additional 2 books per week.
"2 books per week" means 2x
⇒
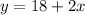 .....[1]
.....[1]
It is also given that Dayton's library started out with 9 books, and he has enough money in his budget to purchase another 3 books per week.
"3 books per week" means 3x
⇒
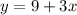 .....[2]
.....[2]
at some points, the two teachers' libraries will contain the same number of books.
⇒
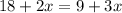
Subtract 9 from both sides we get;
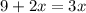
Subtract 2x from both sides we have;
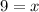
y = 18 + 2x = 18 + 2(9) = 18 + 18 = 36
Therefore,
- 36 books will each class have.