Question

Find d for the sequence for which a1 = 100 and a12 = 34.

a.
-6

b.
6

c.
12

d.
-12


Please select the best answer from the choices provided

a) A
b) B
c) C
d) D

Answer 1

`a_(1)=100, a_(12)=34`

`a_(12)=a_(1)+ 11 d \\\\ 34= 100+11 d\\\\ 34-100=11 d \\\\ -66=11 d \\\\ d=(-66)/(11)\\\\ d=-6`

Option (A) -6 ,is correct common difference.

Answer 2

Option a is correct.

d = -6

Explanation:

An arithmetic sequence defined as the sequence of the number such that the Common difference of any two successive numbers of the sequence is constant.

The formula for nth term in the arithmetic sequence is,

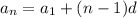`a_n = a_1+(n-1)d` ......[1]

where

`a_1` is the first term.

d is the common difference.

n is the number of terms.

Given that:
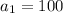`a_1 = 100` and
`a_(12) =34`

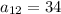
Substitute n =12 and
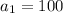`a_1 = 100` in [1] we get

`a_(12) = 100 +(12-1)d`

`a_(12) = 100 +11d`

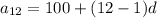
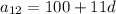
Substitute the value of
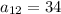`a_(12) =34` to solve for d;'

`34 = 100+11d`

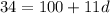
Subtract 100 from both sides we get;

-66 = 11d

Divide both sides by 11 we get;

d = -6

Therefore, the common difference(d) for the given sequence is, -6