Question

Find n for a series for which a1= 30, d = -4, and Sn = -210.

a.
-21

b.
21

c.
-10

d.
10


Please select the best answer from the choices provided

a) A
b) B
c) C
d) D

Answer 1

n= 21 option B

Explanation:

a1= 30, d = -4, and Sn = -210

WE use sum formula

we are given with a1 and d so its arithmetic sequence

the sum formula for arithmetic sequence is

`S_n = (n)/(2)(2a_1 +(n-1)d)`

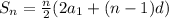
a1= 30 and d= -4 sn =-210

Plug in the values and solve for n

`-210= (n)/(2)(2(30) +(n-1)(-4))`

`-210= (n)/(2)(60-4n+4)`

`-210= (n)/(2)(64-4n)`

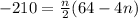
Now distribute the fraction n/2

-210 = 32n - 2n^2

we add 210 on both sides

-2n^2 +32n +210=0

Divide whole equation by -2

`n^2 - 16n - 105=0`

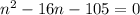
Now we factor left hand side

Product is -105 and sum is -16

-21 times (5) = -105

-21 + (5) = -16

(n-21) (n+5)=0

n -21 = 0 so n= 21

n +5 =0 so n = -5

number of terms cannot be negative so n= 21