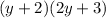Question

Factor by grouping.......................

Answer 1

For this case we have the following xpresion:

`2y ^ 2 + 3y + 4y + 6`

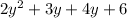
We can rewrite it as:

`2y ^ 2 + 7y + 6`

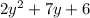
Where:

`a = 2\\b = 7\\c = 6\\`

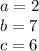
We must factor, for this we follow the steps below:

Step 1:

The term of the medium must be rewritten as the sum of two terms, whose sum is 7 and the product is
`a.c = 2 * (6) = 12`:

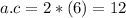Then, the term of the medium, fulfilling the two previous conditions, can be written as:

`4y + 3y`

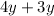
We check:

`4 * 3 = 12\\4 + 3 = 7`

So, we have:

`2y ^ 2 + 4y + 3y + 6`

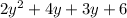
Step 2:

The maximum common denominator (the largest integer that divides them without leaving residue) of each group is factored

`2y ^ 2 + 4y + 3y + 6\\2y (y + 2) + 3 * (y + 2)`

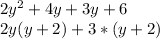
Step 3:

We take common factor
`(y + 2)`:

`(y + 2) (2y + 3)`

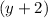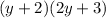
Thus, the expression
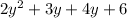`2y ^ 2 + 3y + 4y + 6` can be factored as:

`(y + 2) (2y + 3)`

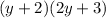
Answer:

`(y + 2) (2y + 3)`