Question

The area of a rectangle is square cm. Find the possible dimensions of the figure, in cm.

Answer 1

(x-1)(8x-3)

Explanation:

`8x^2 - 3x -8x + 3`

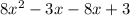
Area of the rectangle is length * width

To find the possible dimension we need to factor the given area

the first parenthesis is length and second parenthesis is width

LEts factor
`8x^2 - 3x -8x + 3`

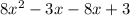
We use grouping method

`(8x^2 - 3x)+(-8x + 3)`

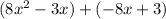
Take out GCf from each group

`x(8x- 3)-1(8x -3)`

(x-1)(8x-3)