Answer:
1. a+c is larger than b+d
2. No way to tell whether a+d or b+c is larger.
Explanation:
1. Which is larger, a+c or b+d?
Let a, b, c, and d be any numbers such that
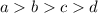 .
.
Specifically, note that
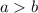 , and subtracting b from both sides of the inequality, observe that
, and subtracting b from both sides of the inequality, observe that
 .
.
Similarly,
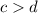 , and subtracting d from both sides of the inequality, observe that
, and subtracting d from both sides of the inequality, observe that
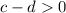 .
.
From this, add "a-b" (a positive number, as proven above) to both sides of the inequality.
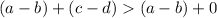
Addition by zero (the additive identity) doesn't change anything, so the right side remains "a-b"...
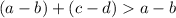
... and "a-b" is positive...
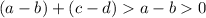
... so, by the transitive property of inequality...
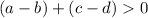
Recall that subtraction is addition by a negative number...
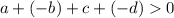
...and that addition is associative and commutative, so things can be added in any order, so the middle two terms on the left side can be rearranged...
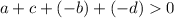
Adding b + d to both sides of the inequality
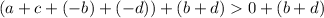
... and simplifying
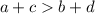
So, a+c is larger than b+d.
2. Which is larger, a+d or b+c?
Consider the following two examples:
Example 1
Suppose a=10; b=3; c=2; d=1.
Note that
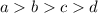 (
(
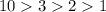 ) and, also observe that
) and, also observe that
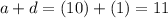 , and
, and
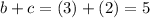 , so a+d is larger than b+c.
, so a+d is larger than b+c.
Example 2
However, suppose a=10; b=9; c=8; d=1.
Note that
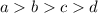 (
(
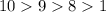 ) but that
) but that
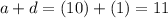 , and
, and
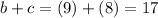 , so a+d is smaller than b+c.
, so a+d is smaller than b+c.
So, in one example, a+d is bigger, and in the other, a+d is smaller. Therefore, there is no way to tell which of a+d or b+c is larger from only the given information.