> Let
 be the height of the ad, and
be the height of the ad, and
 its width. The company wants
its width. The company wants
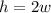 .
.
> Regardless of the size of the ad, the newspaper will charge $50 minimum. Then for every additional $10 for every square inch. This means the price
 of the ad, as a function of the ad's size/area
of the ad, as a function of the ad's size/area
 , is
, is
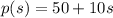
Assuming the ad is rectangular, its size/area is given by
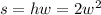 , so we can write the price as a function of the ad's width:
, so we can write the price as a function of the ad's width:

where
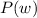 is another price function, but one that depends on
is another price function, but one that depends on
 directly (*not* the same as
directly (*not* the same as
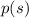 , but represents the same thing).
, but represents the same thing).
> The company wants the price to be no greater than $2050.
So what we're doing is maximizing the size of the ad,
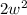 , subject to the price constraint,
, subject to the price constraint,
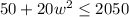 .
.
- - -
Without using calculus (and I won't bother demonstrating the method that does use it): taking the constraint inequality, we can solve for
 to get an idea of what values of
to get an idea of what values of
 are allowed.
are allowed.
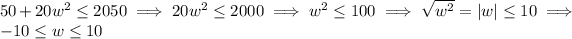
The width of the ad can't be negative, so the actual interval of allowed values for
 would be
would be
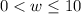 .
.
Since
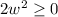 for all
for all
 , it stands to reason that its maximum value will occur at the end of this interval when
, it stands to reason that its maximum value will occur at the end of this interval when
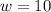 inches.
inches.
The ad's height is twice its width, so the height of the add would be
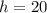 inches, which makes D the correct answer.
inches, which makes D the correct answer.