Answer:
Option D.
Explanation:
Given information:
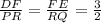 .
.
We need to find the additional information which is needed to prove △DEF ~ △PQR using the SSS similarity theorem.
According to the SSS similarity theorem, two triangles are similar if their corresponding sides are proportional.
Using SSS similarity theorem, both △DEF and △PQR are similar if
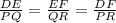
If can be written as
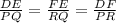
It is given that
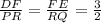 .
.
So, the additional information which is needed to prove △DEF ~ △PQR using the SSS similarity theorem is
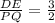 .
.
Therefore, the correct option is D.