Question

The service elevator in a high-rise building travels between the lowest underground parking level and the seventeenth story of the building. The lowest parking level is 15 meters below street level, and the seventeenth story is 51 meters above street level. If the elevator rises at a rate of 2 meters per second, how long, in seconds, could a person ride the elevator when starting from the lowest level? Assume the elevator makes no extra stop.

A. x ≤ 33

B. x ≤ 66

C. x ≤ 18

D. x ≤ 21

Answer 1

15 + 51 = 66 Meters total

`(66)/(2)` = 33 Seconds

A. x
`\leq` 33

Answer 2

x ≤ 33

Explanation:

The lowest parking level is 15 meters below street level

The seventeenth story is 51 meters above street level.

So, the total distance between lowest parking level and seventeenth story = 15+51 = 66 m

Now we are given that the elevator rises at a rate of 2 meters per second

So, the elevator rises 1 m in seconds =
`(1)/(2)`

So, the elevator rises 66 m in seconds =
`(1)/(2) * 66`

=
`33`

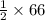
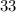
So, the elevator rises 66 m in 33 seconds or less but not more than that

So, Option A is true

x ≤ 33