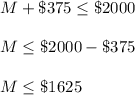Answer: Inequalities will be

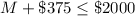
Explanation:
Since we have given that
In First Case :
Number of scores Jenny scored in one part exam = 47
Let the number of scores Jenny scored in second part exam be "P"
And she wants to score in combined exam = atleast 85
So, the system of inequality will be

So, the range of P must be
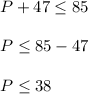
Similarly,
In the second case,
Least amount Tom wants to save for a trip = $2000
Amount he saved so far = $375
Let the amount he needs to save for going for a trip be "M".
So, System of inequality will be
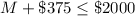
So, Value of M will be