Answer:
Given the statement: Square root 300c^9 = 10c^x square root 3 c
⇒
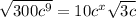
Squaring both sides we get;
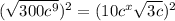
Simplify:
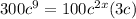
We know:
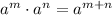
then;
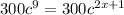
Divide both sides by 300 we get;
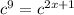
On comparing both sides we have;
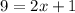
Subtract 1 from both sides we get;
8 = 2x
Divide both sides by 2 we have;
x = 4
Therefore, for the value of x =4 the given statement is true.