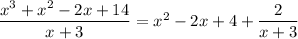First,
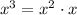 , and if we multiply
, and if we multiply
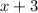 by
by
 we get
we get
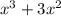
Subtracting this from the numerator gives a remainder of
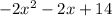
Next,
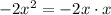 , and if we multiply
, and if we multiply
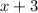 by
by
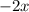 we have
we have
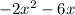
and subtracting this from the previous remainder, we end up with a new remainder of
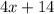
Next,
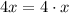 , and if we multiply
, and if we multiply
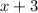 by
by
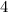 we get
we get
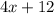
Subtracting from the previous remainder, we get a new remainder of
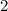
which contains no more factors of
 , so we're done.
, so we're done.
So,