Thomson experiment he calculated the charge to mass ratio just be passing the fundamental charge through a tube
He calculated the charge to mass ratio just by finding the deflection of charge while it is passing through the constant electric field
so here we will use the deflection as following
let say it passes the field of length "L"
so here we have

now in the same time if it deflect by some distance
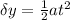
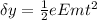
now by solving this equation we can find e/m ratio
so here correct answer will be
the electron's charge-to-mass ratio