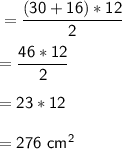Question

-6. The area of trapezium in cm² is A. 276 C. 207 B. 240 D. 225​

Answer 1

276 cm²

Explanation:

Area of trapezium:

Construct a line DE parallel to AB.

DE = 13 cm

So, ABED is a parallelogram

In ΔDEC,

DE = a = 13 cm

EC = AB - BE

= 30 - 16

EC = b = 14 cm

DC = c = 15 cm

Use Heron's formula to find the area of triangle.

`\sf s = (a+b+c)/(2)\\\\=(13+15+14)/(2)\\\\=(42)/(2)\\\\s = 21`

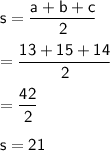
s-a = 21 - 13 = 8

s - b = 21 - 14 = 7

s - c = 21 - 15 = 6

`\sf \boxed{\bf Area \ of \ triangle = √(s(s-a)(s-b)(s-c)) }`

`\sf = √(21 * 8 * 7* 6)\\\\=√(3 * 7 * 2* 2 * 2 * 7 * 2 * 3)\\\\= 3 * 7 * 2 * 2\\\\= 84 \ cm^2`

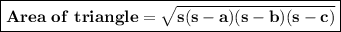
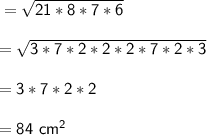
Area of ΔDEC = 84 cm²

`\sf (1)/(2)*base * height = 84\\\\ (1)/(2)*14*height = 84`

`\sf height =(84*2)/(14)\\\\`

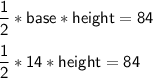
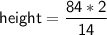
= 6 *2

height = 12 cm

Now we know the height of the trapezium. h = 12 cm

The length of the parallel sides are a = 30 cm & b =16 cm

`\sf \boxed{Area \ of \ trapezium = ((a +b)*h)/(2)}`

`\sf =((30+16)*12)/(2)\\\\=(46*12)/(2)\\\\= 23 * 12\\\\= 276 \ cm^2`