Question

Five kids from the neighborhood are heading to the store to get some snacks. Kid #1 jas $1, kid #2 has $2, kid #3 has $3, kid #4 has $4, and kid #5 has $5. What is the average (mean) amount of cash the five kids have? What's the median?

Two weeks later the family of kid #5 won the lottery and the kids got together to go to the store to get some snacks again. This time around kid #1 has $1, kid #2 has $2, kid # 3 has $3, kid # 4 has $4, and kid #5 has a waffle of cash totals $5,000. What is the average (mean) amoint of cash the five kids have this time? Whats the median?

From part a, how have the mean and the median changed? Which one -the mean or the median- os a better reflection of how much money the neighborhood kids have?

Answer 1

Median is a better reflection of how much money the neighborhood kids have.

Explanation:

We have been given that 5 kids from the neighborhood are heading to the store to get some snacks. Kid #1 has $1, kid #2 has $2, kid #3 has $3, kid #4 has $4, and kid #5 has $5.

`\text{Mean}=\frac{\text{Sum of all the numbers}}{\text{All the number in data set}}`

`\text{Mean}=(1+2+3+4+5)/(5)`

`\text{Mean}=(15)/(5)`

`\text{Mean}=3`

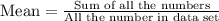
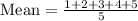
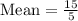
Therefore, the average (mean) amount of cash the five kids have this time is $3.

Median of data set : $1, $2, $3, $4, $5.

Our data set has 5 data points, so median will be the value of 3rd data point, which is 3, therefore, median of data set is $3.

Now let us find mean of data set after the family of kid #5 won the lottery.

`\text{Mean}=(1+2+3+4+5000)/(5)`

`\text{Mean}=(5010)/(5)`

`\text{Mean}=1002`

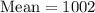
Therefore, the mean after replacing $5 by $5,000 will be $1002.

Median of new data set : $1, $2, $3, $4, $5000.

Our new data set has 5 data points, so median will be the value of 3rd data point, which is 3, therefore, median of the new data set is still $3.

Since mean is affected by a very small or large valued data point. We have seen this by the change in kid #5's money as our mean of the money has changed from $3 to $1002, while median remained same, therefore, median is the better reflection of how much money the neighborhood kids have.