Answer:
See graph in attachment
Explanation:
We want to graph the function,
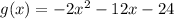
First, let us rewrite the function in the vertex form;
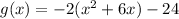
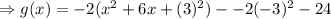
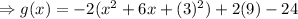
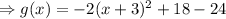

The parabola opens downwards because
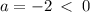
The vertex of the parabola is
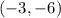 .
.
At y-intercept,
 .
.
This implies that,
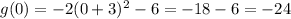
At x-intercept,

This implies that;
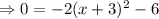
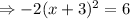
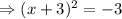
This equation has no real number solutions because of
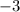 on the right hand side. This implies that the graph has no x-intercepts.
on the right hand side. This implies that the graph has no x-intercepts.
We therefore draw a maximum graph through the vertex and the y-intercept to obtain the graph in the attachment.