Question

Select all radical expressions that are equivalent to 3 4/7

Sorry for the bad quality!!

Answer 1

`(\sqrt[7]{3} )^(4)`

Explanation:

The only radical that matches the equivalent answer is the fifth one down. We can easily eliminate the radicals without exponents on the outside, since we know they won't create leftover fractions. So that leaves us with the second, fourth and fifth answers to contemplate.

Let's look at
`(\sqrt[4]{3} )^(7)` and
`\sqrt[4]{3^(7) }` first. It's good to know that these are equivalent radicals. The numbers are the same, and they will produce the same answers.

When you do the math, the exponent rule gives us fractions of
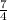`(7)/(4)` for exponents, and eventually, a
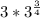`3 * 3^{(3)/(4) }` for both answers. So these are eliminated.

Now, for
`(\sqrt[4]{3}^(7)`, we can easiy simplify by changing the 7th root to a fraction in our exponent. Use the rule:
`\sqrt[n]{x} = x^{(1)/(n) }`

1. 
   `(3^{(1)/(7) } )^(4)`
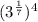
2. Multiply the exponents:
   `(1)/(7) * 4 = (4)/(7)`
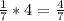
3. Insert the product into the exponent:
   `3^{(4)/(7) }`

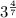
And we can see the answer we're looking for! If you use this method to look at the other problems, you'll see that this is the only radical that simplifies to the required answer.

Answer 2

Correct \/

Explanation:

I just took the test