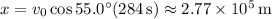The shell's horizontal position
 and vertical position
and vertical position
 are given by
are given by
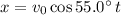
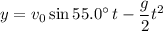
where
 is the given speed of 1.70 x 10^4 m/s, and
is the given speed of 1.70 x 10^4 m/s, and
 is the acceleration due to gravity (taken here to be 9.80 m/s^2).
is the acceleration due to gravity (taken here to be 9.80 m/s^2).
To find the horizontal range, you can use the range formula,
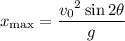
with
 being the angle at which the shell is fired.
being the angle at which the shell is fired.
Alternatively, we can work backwards and deal with part (b) first:
(b) The time spent in the air is the time it takes for the shell to reach the ground. To find that, you solve for
 in
in
 :
:
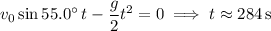
(a) After this time, the shell will have traveled horizontally