Question

Lim x-π/4 x(cos³x-sin³x)/(tan4xcosx)

Answer 1

For starters, we can write

`\cos^3x-\sin^3x=(\cos x-\sin x)(\cos^2x+\cos x\sin x+\sin^2x)=(\cos x-\sin x)(1+\cos x\sin x)`

Then we can absorb the factor of
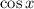`\cos x` from the denominator into the numerator:

`(x(\cos^3x-\sin^3x))/(\tan4x\cos x)=(x(1-\tan x)(1+\cos x\sin x))/(\tan 4x)`

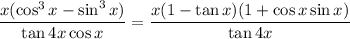
Then provided that

`\displaystyle\lim_(x\to\pi/4)(1-\tan x)/(\tan4x)`

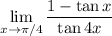
exists, we can split the limit of the product into the product of limits:

`\displaystyle\lim_(x\to\pi/4)(x(\cos^3x-\sin^3x))/(\tan4x\cos x)=\left(\lim_(x\to\pi4)x(1+\cos x\sin x)\right)\left(\lim_(x\to\pi4)(1-\tan x)/(\tan 4x)\right)`

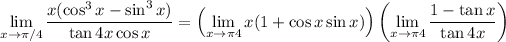
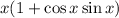`x(1+\cos x\sin x)` is continuous at
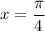`x=\frac\pi4`, so that limit reduces to
`\frac\pi4\left(1+\cos\frac\pi4\sin\frac\pi4\right)=\frac{3\pi}8`.

The remaining limit is of indeterminate form 0/0; one application of L'Hopital's rule shows that the limit would be

`\displaystyle\lim_(x\to\pi/4)(1-\tan x)/(\tan4x)=\lim_(x\to\pi/4)(-\sec^2x)/(4\sec^24x)=-\frac12`

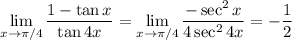
so the final limit would be
`-(3\pi)/(16)`.

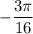But if you haven't learned about L'Hopital's rule (or if you're like me and prefer doing more work for some reason), we have to try something else: more trig identities!

Euler's formula and DeMoivre's theorem are very useful here:

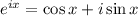`e^(ix)=\cos x+i\sin x` (Euler)

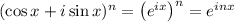`(\cos x+i\sin x)^n=\left(e^(ix)\right)^n=e^(inx)` (DeMoivre)

Take
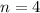`n=4`; then

`e^(4ix)=\cos4x+i\sin4x=(\cos^4x-6\cos^2x\sin^2x+\sin^4x)+i(4\cos^3x\sin x-4\cos x\sin^3x)`

`\implies\begin{cases}\cos4x=\cos^4x-6\cos^2x\sin^2x+\sin^4x\\\sin4x=4\cos^3x\sin x-4\cos x\sin^3x\end{cases}`

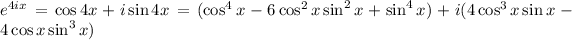
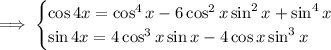
So we have

`\tan 4x=(4\cos^3x\sin x-4\cos x\sin^3x)/(\cos^4x-6\cos^2x\sin^2x+\sin^4x)`

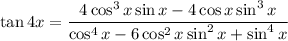
On the right side, divide through the numerator and denominator by
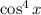`\cos^4x`; doing so yields

`\tan 4x=(4(\sin x)/(\cos x)-4(\sin^3x)/(\cos^3x))/(1-6(\sin^2x)/(\cos^2x)+(\sin^4x)/(\cos^4x))`

`\implies\tan4x=(4\tan x-4\tan^3x)/(1-6\tan^2x+\tan^4x)=(4\tan x(1-\tan x)(1+\tan x))/(1-6\tan^2x+\tan^4x)`

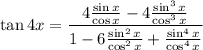
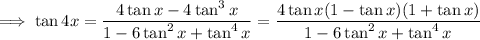
So in the limit, we can simplify the rational expression even further:

`\displaystyle\lim_(x\to\pi/4)(1-\tan x)/(\tan4x)=\lim_(x\to\pi/4)(1-\tan x)/((4\tan x(1-\tan x)(1+\tan x))/(1-6\tan^2x+\tan^4x))=\lim_(x\to\pi/4)(1-6\tan^2x+\tan^4x)/(4\tan x(1+\tan x))`

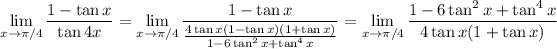
and this function happens to be continuous at
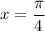`x=\frac\pi4`, so we can evaluate directly:

`\displaystyle\lim_(x\to\pi/4)(1-\tan x)/(\tan4x)=(1-6\tan^2\frac\pi4+\tan^4\frac\pi4)/(4\tan\frac\pi4\left(1+\tan\frac\pi4\right))=-\frac48=-\frac12`

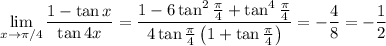
We end up with the same limit we found earlier,
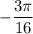`-(3\pi)/(16)`.