Answer:
The ratio of the length of the side opposite the 30°angle to the length of the side opposite the 90°angle is 1:2.
Explanation:
Consider ABC, With 90° angle at B and 30° angle at C.
To find: AB:AC=?
Solution:
AB = perpendicular of the right angled triangle
AC = Hypotenuse of the triangle
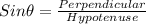
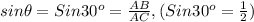

The ratio of the sides ,AB:AC = 1:2.
Hence,the ratio of the length of the side opposite the 30°angle to the length of the side opposite the 90°angle is 1:2.