If you're just starting calculus, perhaps you're asking about using the definition of the derivative to differentiate
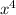 .
.
We have
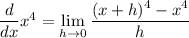
Expand the numerator using the binomial theorem, then simplify and compute the limit.
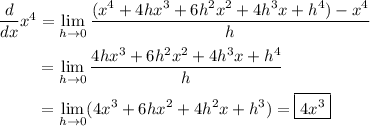
In general, the derivative of a power function
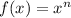 is
is
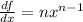 . (This is the aptly-named "power rule" for differentiation.)
. (This is the aptly-named "power rule" for differentiation.)