1 Answer

Andrej Panjkov · Answer 1 · 2020-07-02T01:11:49+0000

Answer:

The equation of the graph below is:

$y=\cos (x+\pi)$

Clearly from the graph that is provided to us we observe that when x=0 the value of the cosine function is: -1

Hence, we put x=0 in each of the given options and check which hold true.

A)

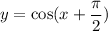
$y=\cos (x+(\pi)/(2))$

when x=0 we have:

$y=\cos ((\pi)/(2))\\\\\\y=0\\eq -1$

Hence, option: A is incorrect.

B)

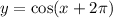
$y=\cos (x+2\pi)$

when x=0 we have:

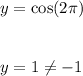
$y=\cos (2\pi)\\\\\\y=1\\eq -1$

Hence, option: B is incorrect.

C)

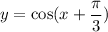
$y=\cos (x+(\pi)/(3))$

when x=0 we have:

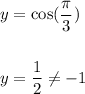
$y=\cos ((\pi)/(3))\\\\\\y=(1)/(2)\\eq -1$

Hence, option: C is incorrect.

D)

$y=\cos (x+\pi)$

when x=0 we have:

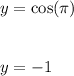
$y=\cos (\pi)\\\\\\y=-1$

Similarly by the graph of the function we see that it matches the given graph.

Hence, option: D is correct.