SOLVING
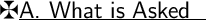
Perform the indicated operation and write the answer with the form a+bi.
2 numbers given, one of which is complex

Multiply these two numbers, just like you always multiply binomials.
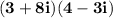 | multiply
| multiply
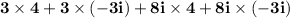 | simplify
| simplify
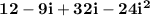 | this can be simplified A LOT
| this can be simplified A LOT
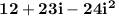 | as strange as it may seem, this can be simplified even more, because isn't i^2 the same as -1?
| as strange as it may seem, this can be simplified even more, because isn't i^2 the same as -1?
 | add 12 and 24
| add 12 and 24
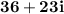

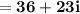 . The answer is written in the form a+bi, as requested.
. The answer is written in the form a+bi, as requested.