Question

Please help!!

Consider the system
{12x+3y=40
7x-4y=38
a. Explain how you know there is a unique solution to this system.

b. Explain how you can tell that the point (2.5, -3.4) is not a solution to the system.

Answer 1

The two linear equations in two variable is:

12 x + 3 y = 40

7 x - 4 y = 38

(a) For a system of equations in two Variable

a x + by = c

p x + q y = r

It will have unique solution , when

`(a)/(p)\\eq (b)/(q)\\eq(c)/(r)`

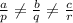
As, you can see that in the two equation Provided above

`(12)/(7)\\eq (3)/(-4)\\eq (40)/(38)`

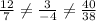
So, we can say the system of equation given here has unique solution.

(b). If point (2.5, -3.4) satisfies both the equations, then it will be solution of the system of equation, otherwise not.

1. 12 x+3 y=40

2. 7 x-4 y=38

Substituting , x= 2.5 , and y= -3.4 in equation (1) and (2),

L.H.S of Equation (1)= 1 2 × 2.5 + 3 × (-3.4)

= 30 -10.20

= 19.80≠ R.H.S that is 40.

Similarly, L H S of equation (2)= 7 × (2.5) - 4 × (-3.4)

= 17.5 +13.6

= 31.1≠R HS that is 38

So, you can Write with 100 % confidence that point (2.5, -3.4) is not a solution of this system of the equation.