Question

James just began a job as a nurse. He is given a starting salary of $66,640 per year. He is also told that his salary will increase to $73,400 in 8 years. Assume that x = the years worked and y = Salary in dollars. Using this information, find the following answers: What is the rate of change of James’ salary? Instructions: Find the slope by first creating two points in the form (years, salary), and then calculate the slope using the correct slope formula.

Create the slope-intercept equation of the line that represents James’ salary.

Include an explanation of what the variables represent and how you know their placement.
Using your equation in (2), find the value of James’ salary in 23 years.

Answer 1

the rate of change of James’ salary is $845 dollars per year

y = 845x + 66640

the value of James’ salary in 23 years=$86,075

Explanation:

Let x = the years worked and y = Salary in dollars

When x=0 then y = 66640

when x= 8 then y = 73400

Two points are (0,66640) and (8,73400)

Rate of change of salary is the slope

To find slope we use formula

`slope = (y_2-y_1)/(x_2-x_1) =(73400-66640)/(8-0) =845`

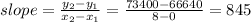
the rate of change of James’ salary is $845 dollars per year

Slope intercept form of equation is y=mx+b

m = 845 , b is the y intercept (initial salary)

so y = 845x + 66640

Now we find out salary in 23 years

plug in 23 for x in the y equation

y = 845x + 66640

y = 845(23) + 66640=86075

the value of James’ salary in 23 years=$86,075