Question

Triangle TUV and triangle LMN are similar what is the measure of side LM

Answer 1

28cm

Step-by-step explanation: First find the ratio of the sides

6/21=8/?

you can simplify that to 2/7=8/x

The cross multiply to get 56=2x

Then divide 56 by to 2 get 28=x

Answer 2

Side LM has a length of 28 centimeters.

Explanation:

Similar triangles are those that are related by a proportion, that is, they have a scale ratio in common.

You can notice in the image that the given triangles are similar, that means we can deduct the proportion

`(TV)/(LN)=(TU)/(LM)`

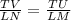
Replacing each value, we have

`(6)/(21)=(8)/(x)`

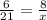
Then, we solve for
`x`

`6x=168\\x=(168)/(6)\\ x=28`

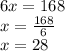
And,
`LM=x=28`

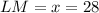
Thereofore, side LM has a length of 28 centimeters.