Each leg of a 45°- 45°- 90° triangle measures 14 cm. What is the length of the hypotenuse?

Question

asked Jan 21, 2020 95.4k views

2 Answers

Farbodg · Answer 1 · 2020-01-28T04:02:27+0000

Answer: 19.79 cm

Explanation:

1. To solve the exercise you must apply the Pythagorean Theorem as you can see below:

$a=\sqrt{b^(2)+c^(2)}$

Where a is the hypotenuse and b and c are the legs.

2. Then, you must substitute values:

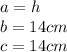
$a=h\\b=14cm\\c=14cm$

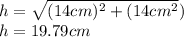
$h=\sqrt{(14cm)^(2)+(14cm^(2)})\\h=19.79cm$

3. The length of the hypotenuse is 19.79 centimeters.