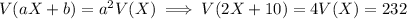What I gather from the question is that
 has second moment
has second moment
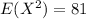 and variance
and variance
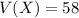 , and you're asked to find the expectation and variance of the random variable
, and you're asked to find the expectation and variance of the random variable
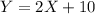 .
.
From the given second moment and variance, we find the expectation of
 :
:
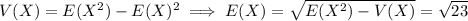
Expectation is linear, so
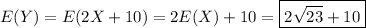
Using the same variance identity, we have
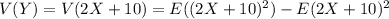
and
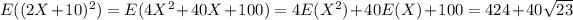
so that

Alternatively, we can use the identity