Question

Two water pumps are filling a pool. One of the pumps is high power and can fill the pool 5 hours before the other can do. However, they both working together can fill half of the pool in 3 hours. In how many hours the high power pump can fill the pool

Answer 1

L = hours for the slower pump to fill the pool

L - 5 = hours for the high power pump, since it can do it in 5 hours less.

since the slower pump takes L hours, the faster pump takes then L - 5 hours.

we know both pumps together take 3 hours to do half of the pool, so that means that to fill up the whole pool it takes them 6 hours.

since the slower pump can do it alone in L hours, in 1 hour it has done 1/L of the whole thing.

likewise, since the faster pump can do it in L-5 hours, in 1 hour alone it has done 1/(L-5) of the whole job.

`\bf \stackrel{\textit{slower pump's rate}}{\cfrac{1}{L}}~~~~+\stackrel{\textit{faster pump's rate}}{\cfrac{1}{L-5}}~~~~=~~~~\stackrel{\textit{total done in 1 hour}}{\cfrac{1}{6}} \\\\\\ \textit{let's multiply both sides by }\stackrel{LCD}{6(L)(L-5)}\textit{ to do away with the denominators} \\\\\\ 6(L)(L-5)\left( \cfrac{1}{L}+\cfrac{1}{L-5} \right)=6(L)(L-5)\left( \cfrac{1}{6} \right)`

`\bf 6(L-5)+6L=(L)(L-5)\implies 6L-30+6L \\\\\\ 12L-30=L^2-5L\implies 0=L^2-17L+30 \\\\\\ 0=(L-15)(L-2)\implies L= \begin{cases} \boxed{15}\\ 2 \end{cases}`

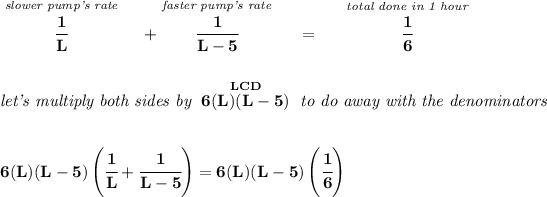
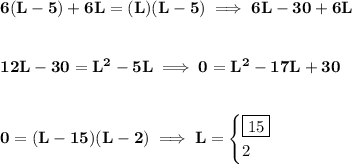
now, we can't use L = 2, because, the whole job by both is done in 6 hours, there's no way the slower pump can do it in less than that, so L = 15.

now if L = 15, then L - 5 = 10.