Both angles ABO and ADO are right angles because ABP and ADQ are tangent to circle O. The interior angles of a quadrilateral add up to 360 degrees, so the measure of angle BOD (and measure of minor arc BD, denoted
 ) is
) is

This also means the measure of the central angle BOD that subtends major arc BCD (also the measure of the major arc BCD is)
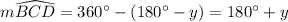
The inscribed angle theorem says that the measure of angle BOD is twice the measure of angle BCD, so
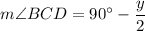
The interior angles of quadrilateral BCDO have sum
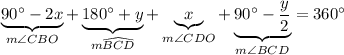
Simplifying this equation will give you
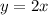 .
.