Answer:
The value of x is
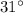 .
.
Explanation:
Please look at the figure attached to get more clear solution.
We have given:
FG||CB
And the line that cut the parallel line is transversal so, here BA is transversal
And alternate interior angles on transverse line are equal
So, ∠1=∠4
And ∠4=
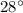
Hence, ∠1=∠4=
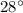
And On FG the sum of angles will be

∠3+∠2+∠1=

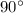 +∠2+
+∠2+
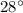 =
=

Hence, ∠2=
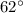
Now, we know that the sum of interior angles is equal to the exterior angle:
Therefore, ∠2+∠5=∠6+∠7
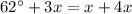
On simplification we get:

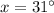
Hence, the value of x is
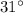 .
.