Answer:
The corresponding side of the first triangle is 4 m.
Explanation:
In similar triangle, ratio of areas of triangles is equal to the ratio of square of their corresponding sides.
Consider, the below two similar triangles,
area(ΔXYZ) = 20m² , area(ΔPQR) = 180m² and PQ = 12m
We have to find value of XY.
According to above property of similar triangle,
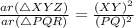
Put values in the above equation, we get,
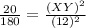
Solving for XY,
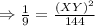
Cross multiply, we get,
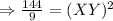
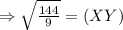
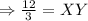
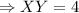
Thus, the corresponding side of the first triangle is 4 m.