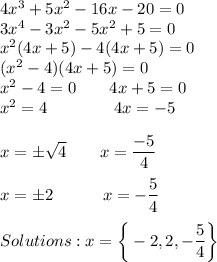NOTES: To find the intercepts/roots:
- move everything to one side and 0 on the other
- factor the equation
- apply the Zero Product Property (set each factor equal to 0)
- solve for x
11. Answer: x = {-4, 0, 5}
Explanation:
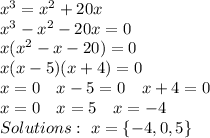
***********************************************************************************
12. Answer: x = No real solution
Explanation:
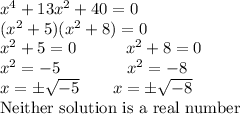
***********************************************************************************
13. Answer: x = {-2, 2}
Explanation:
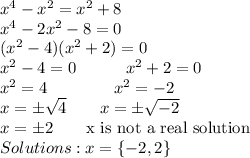
***********************************************************************************
14. Answer:
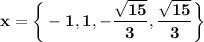
Explanation:
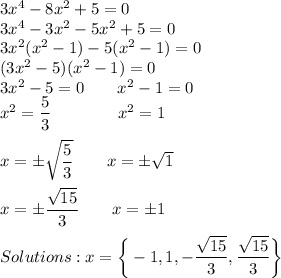
***********************************************************************************
15. Answer:
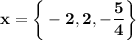
Explanation: