Question

Help please with this math

Answer 1

Option third is True.

Explanation:

We have been given the exponential expression
`3m^{(7)/(9)}`

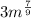
The exponent 7/9 is with the variable m only, not on 3. Hence, option first is not correct.

Also rational exponent is 7/9. Hence, second option is also incorrect.

Now, we can rewrite the expressions as

`3m^{(7)/(9)}=(m^7)^{(1)/(9)}`

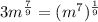
Now, using the rule
`x^{(1)/(n)}=\sqrt[n]{x}`

`3m^{(7)/(9)}=\sqrt[9]{m^7}`

Hence, 9 is the index

Therefore, option third is True.