Answer: Triangle ABC is similar to triangle EDC because Measure of angle 3 equals measure of angle 4 and Measure of angle 1 equals measure of angle 5
Explanation:
Given:
 ,
,
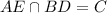
Where AE and BD are the common transversals of parallel lines AB and DE,
Also, Angle CAB is labeled 1, angle ABC is labeled 2, angle ACB is labeled 3, angle DCE is labeled 4, angle CDE is labeled 6, and angle CED is labeled 5.
Thus,
 ( Vertically opposite angles )
( Vertically opposite angles )
 ( Alternative interior angle theorem)
( Alternative interior angle theorem)
Thus, By AA similarity postulate,
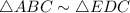
Hence, proved.
Second Option is correct.