Question

Find and correct the error of the following factor.

Answer 1

C. The greatest common factor was not factored out correctly from second group

Explanation:

The following lines show the process of factorization by using common factor.

Line 1:

In line 1, the equation is given and is grouped from which common factors can be taken. This is completely fine.

`(3x^(2)+xy^(2)) +(-3xy-y^(3) )=0`

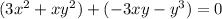
The only thing missing was equate to zero, but the options below talk about correct factors only, therefore this can't be considered as a mistake and can be ignored completely.

Line 2:

In line 2, the common terms are taken out from groups. The common term x is taken from group 1 which is fine. In second group the common term -y is taken out, which is fine but it was not factored out correctly. The correct factorization would have been:

`x(3x+y^(2)) -y(3x +y^(2) )=0`

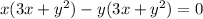
which is different from what is given in line 2.

Options:

A. The grouping is correct in line 1. So this option is does not hold.

B. Common factor was factored correctly from group 1. So this option does not hold.

C. Common factor was not factored correctly from group 2. So this option holds and is correct. Thus we choose this option as correct answer.

D. There is a mistake. So this option is also not correct.