Answer:
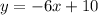
Explanation:
The point of intersection of
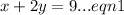
and

is the solution of the two equations.
We add equation (1) and equation(2) to get,
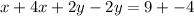
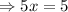

We put
 into equation (1) to get,
into equation (1) to get,
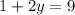
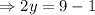
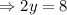
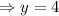
Therefore the line passes through the point,
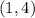 .
.
The line also passes through the point of intersection of
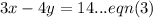
and
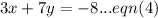
We subtract equation (3) from equation (4) to obtain,

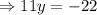
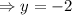
We substitute this value into equation (4) to get,
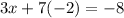
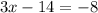
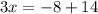
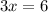

The line also passes through

The slope of the line is
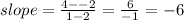
The equation of the line is


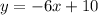 is the required equation
is the required equation