Question

40% of Oatypop cereal boxes contain a prize. Hannah plans to keep buying cereal until she gets a prize. What is the probability that Hannah only to buy 3 or less boxes before getti g a prize? We need to design a simulation. Which random can we use to best represent this situation

Answer 1

Use a random number generator ranging from 1 to 10 and assign 1 to 4 as the prize and 5 to 10 as no prize.

Answer 2

The percent probability of winning a prize=40%.

and not winning prize=60%.

We are asked to find the probability that Hannah only has to buy 3 or less boxes before getting a prize.

Let the random used is x=0,1,2,3 ( where

• 0 denotes that we got the success in first attempt.
• 1 denotes that first bag does not contain prize but we get success in second attempt.
• 2 denotes that we did not get success in 2 attempts but in third we get the success.
• 3 denotes that the success is not obtained in any of the three attempts )

Hence, the probability that the first box will contain prize=
`(40)/(100)`

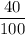
The probability that the first box will not contain prize but second will=
`(60)/(100)*(40)/(100)`

The probability that the first and second box will not contain prize but third will=
`(60)/(100)*(60)/(100)*(40)/(100)`

The probability that the first and second box will not contain prize but third will=
`(60)/(100)*(60)/(100)*(40)/(100)`

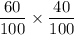
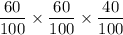
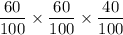
The probability that the prize is not contained in first, second and third box=
`(60)/(100)+*(60)/(100)*(60)/(100)`

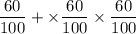
Hence, the total probability=

`(40)/(100)+(60)/(100)*(40)/(100)+(60)/(100)*(60)/(100)*(40)/(100)+(60)/(100)+*(60)/(100)*(60)/(100)`