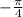ANSWER
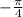
Step-by-step explanation
The given function is,
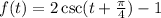
This function has a period of

just as the parent function
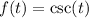
A sample period of this parent function is
![[ 0 , 2\pi]](https://img.qammunity.org/2020/formulas/mathematics/high-school/iss1alw9pgar6p6mx0r2nioxbxn4gk61y1.png)
Which begins at zero.
For the transformed function,
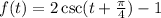
There has been a horizontal shift of
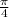
to the left.
The transformed function will have a sample period,
![[ - (\pi)/(4) , (7\pi)/(4) ]](https://img.qammunity.org/2020/formulas/mathematics/high-school/c6ublastjh83u2ga8sjzdanjdu0yq80igq.png)
Therefore a sample period begins at