Question

Two planes start flying towards each other simultaneously from two different cities. The distance between the cities is 960 miles and one of the planes' speed exceeds the other by 75 mph. If after 1.5 hours of the flight they were still 75 miles apart, what were the speeds of the planes, in mph?

Answer 1

The speed of one plane = 257.5 miles per hour

And speed of second plane = 332.5 miles per hour

Explanation:

We have given,

Distance between two cities = 960 miles

Two planes are flying towards each other.

Let the speed of one plane be x.

Then,

Speed of second plane = x+75 {Following this "one of the planes' speed exceeds the other by 75 mph"]

After 1.5 hours they are still 75 miles apart.

i.e Relative distance between two planes = Relative speed of plane × Time

Here

relative speed = x + (x+75) , and relative distance left to cover = 960-75.

i.e

(960 - 75) = {x+(x+75)}×1.5

885 = (2x+75)×1.5

or
`(885)/(1.5) =2x+75`

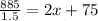
or 590-75 = 2x

or 515 = 2x

or x =
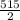`(515)/(2)` = 257.5

Hence the speed of one plane = x = 257.5 miles per hour

And speed of second plane = (x+75) = 257.5 + 75 = 332.5 miles per hour