Answer: The answer is (C) 324 cubic cm.
Step-by-step explanation: As given in the question, given a solid oblique pyramid with a regular hexagonal base and area 54√3 cm². Also, the edge length of the base is 6cm and ∠BAC = 60°.
We are to find the volume of the pyramid.
The formula for finding the volume of a pyramid is given by
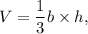
where, 'b' is the base area and 'h' is the perpendicular height of the pyramid.
Here, b = 54√3 cm², h = ?
Now, from the right-angled triangle ABC, we have
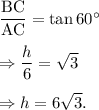
Therefore, the volume of the pyramid is
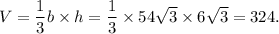
Thus, the required volume is
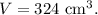 This makes (C) as the correct option.
This makes (C) as the correct option.